Será que é possível resolver enigmas matemáticos sem fazer contas?
Espaçonaves cúbicas e números hexagonais
Para começar essa história, apresento a você os personagens principais. Aqui temos os números hexagonais, ou melhor, os quatro primeiros:

As bolinhas são todas idênticas e estão arranjadas nesse formato de hexágono, representado os números: 1, 7, 19 e 37.
Agora vamos às espaçonaves cúbicas, que são formadas por cubinhos:
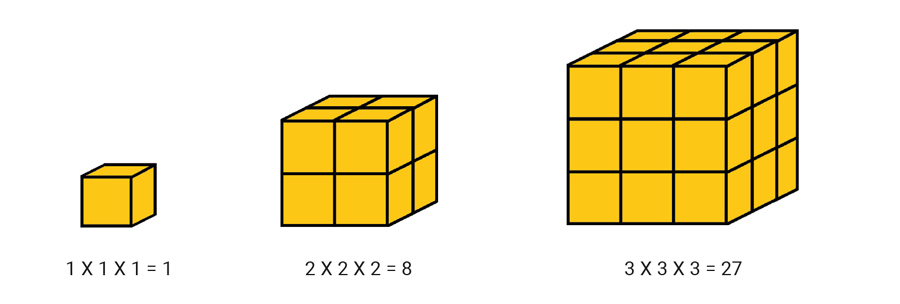

Pedro Roitman,
Instituto de Matemática,
Universidade de Brasília
Sou carioca e nasci no ano do tricampeonato mundial de futebol – para quem é muito jovem, isso aconteceu em 1970, século passado! Enquanto fazia o curso de Física na universidade, fui encantado pela Matemática. Hoje sou professor.
Edição Exclusiva para Assinantes
Para acessar, faça login ou assine a Ciência Hoje das Crianças
admin
CONTEÚDO RELACIONADO

Que comecem os Jogos! E o respeito à natureza
Qual a mensagem que os Jogos Olímpicos de 2024 querem passar ao mundo?



