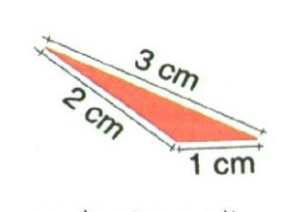
Se alguém pergunta qual é o perímetro, isto é, qual é o resultado da soma dos lados do triângulo abaixo, a resposta é moleza. Basta somar: 1 centímetro + 2 centímetros + 3 centímetros  e o resultado será 6 centímetros.

(imagem: Nato Gomes)

Mas se alguém pedisse para você dar conta de somar os lados de uma couve-flor? Você acharia que isso não é pergunta que se faça? Pois faz algum tempo que os biólogos vêm tentando medir árvores, arbustos, corais, algas, esponjas-do-mar e vários outros organismos vivos que servem de morada para os mais diferentes bichos.

O objetivo desse estudo, que mistura biologia e geometria, é descobrir como as formas dos ambientes influenciam os animais na escolha do local para viver, oferecendo proteção contra predadores, abrigo contra as variações climáticas e alimento.

Aqui entra a geometria fractal, aquela que, diferentemente da geometria que aprendemos na escola, não se propõe a medir superfícies lisas, como um quadrado ou um cone, mas, sim, superfícies muito irregulares, que podem ser até consideradas enrugadas, como a superfície de uma árvore, de uma couve-flor ou de uma esponja.

(foto: Rizki Ekananda / Flickr / (a href=https://creativecommons.org/licenses/by/2.0/deed.pt)CC BY 2.0(/a))

Na matemática, fractal é um objeto que se apresenta igual aos nossos olhos por mais que nos aproximemos ou nos afastemos dele, algo como um quadro dentro de um quadro, dentro de um quadro, infinitamente. Bem, se um quadro sempre reproduz um quadro menor dentro dele, ao tentarmos medir o comprimento da figura formada por todos os quadros, chegaremos à conclusão de que este tamanho é infinito, certo?

Mas o que isso tem a ver com a couve-flor, com a árvore ou com a esponja? Todos esses são exemplos de fractais porque o comprimento e a área (ou o tamanho) deles são crescentes conforme tentamos medi-los com maior precisão, ou seja, conforme vamos incluindo cada vez mais detalhes de suas formas na nossa medição.

Imagine um compasso. Para tentar preencher o contorno da copa de uma árvore com uma sequência de segmentos de reta do tamanho da abertura do compasso, bastaria multiplicar o número de segmentos necessários para medir toda a árvore pelo tamanho da abertura do compasso, que você chegaria ao comprimento estimado daquele contorno.

Mas e se você resolvesse fazer essa medida com maior precisão e diminuísse a abertura do compasso? Você conseguiria reproduzir com maiores detalhes o contorno da copa e o comprimento final seria ainda maior. E assim aconteceria, sucessivamente, cada vez que você diminuísse mais a abertura do compasso.

As linhas entre as árvores mostram o tamanho da abertura de um compasso usado para medir o contorno delas. Quanto menor a abertura, maior o comprimento encontrado. (imagem: Nato Gomes)

Esse aumento de tamanho só é crescente porque você está tentando medir o perímetro de uma curva muito complexa. Se você experimentar fazer a mesma coisa com uma reta, verá que o comprimento será sempre o mesmo, porque se trata de uma curva regular.

Depois de tantas medições, é provável que você esteja se perguntando que importância tem isso para os animais. Uma importância muito grande, pois cada curva da árvore pode ser entendida como um refúgio para os animais que vivem nela e precisam se proteger do vento, dos predadores… Acontece que nem todos os refúgios servem para todos os animais e, sim, são compatíveis com o tamanho de cada um deles.

Quanto mais recortado for o contorno dos galhos de uma árvore – ou de qualquer outro tipo de habitat que você imagine –, maior a quantidade de refúgios para animais pequenos, que tendem a aparecer em maior quantidade ali por serem os únicos capazes de se utilizar daqueles pequenos abrigos disponíveis no ambiente.

(Esta é uma reedição do texto publicado na CHC 110)