Muitas crianças, aposto, já se depararam com esta tarefa na aula de geografia: colorir um mapa. Quantas cores temos que usar para deixá-lo bem bonito, sem que duas regiões de mesma cor encostem uma na outra? Essa é a dificuldade em colorir mapas – afinal, cada região tem que ficar clara só de bater o olho. Talvez você se surpreenda com o que vou dizer agora, mas esta questão intrigou os matemáticos por muito tempo!
Tudo começou quando o matemático sul-africano Francis Guthrie (1831-1899) estava brincando de colorir o mapa da Inglaterra. Ele percebeu que, com apenas quatro cores, conseguia completar a tarefa, e ficou se perguntando se isso seria verdade para qualquer mapa. A brincadeira virou um problema matemático interessante.
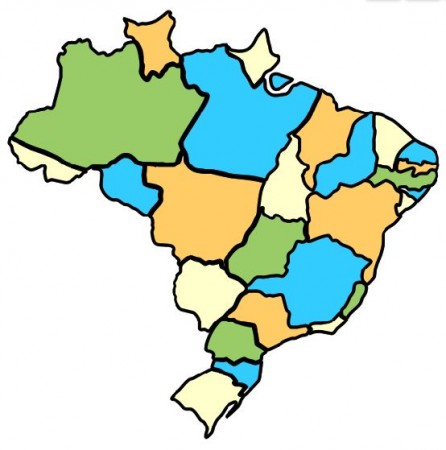
Usando apenas quatro cores, é possível pintar um mapa do Brasil sem que dois estados que fazem fronteira um com o outro fiquem da mesma cor.
Francis não conseguiu provar que quatro cores bastavam para qualquer mapa. Pediu a ajuda, então, a seu irmão, Frederick Guthrie (1833-1886), que era físico e químico. Frederick, por sua vez, passou a bola para um de seus professores, o grande matemático britânico Augustus De Morgan (1806-1871). Daí em diante, muita gente começou a pensar sobre a questão.
A solução só apareceu em 1976, graças aos matemáticos Kenneth Appel e Wolfgang Haken. Para resolver de vez o problema das quatro cores, eles fizeram algo inovador: usaram computadores na solução e produziram mais de mil páginas de material. Ficou provado, então, que qualquer mapa pode ser colorido com quatro cores, sem que duas regiões de mesma cor façam fronteira uma com a outra.
Existem, por outro lado, algumas situações em que menos de quatro cores bastam. Veja, abaixo, o mapa – sim, para os matemáticos é um mapa! – formado pela interseção de vários círculos. Ele pode ser colorido com apenas duas cores. Experimente!
Pode ser que você tenha começado assim: pintou alguma região de vermelho e, depois, as que fazem fronteira com ela de azul, e continuou assim até o mapa ficar todo colorido, certinho, de vermelho e azul. Funciona! Mas o problema, na verdade, é provar que esse método funciona sempre. Existe um jeito? Claro que sim.
Escolha um ponto qualquer dentro do mapa – ele estará no interior de um ou mais círculos. Então, pinte o mapa seguindo esta regra: se o ponto estiver dentro de um número par de círculos, pinte a região de azul; se o número de círculos for ímpar, use vermelho.
E por que isso funciona sempre? Bem, imagine que escolhemos um ponto englobado por um número par de círculos. Se atravessarmos uma de suas fronteiras, estaremos sempre saindo de um dos círculos ou entrando em um novo círculo. Como nossa região inicial estava no interior de um número par de círculos, então, de qualquer forma, passaremos para uma região englobada por um número ímpar de círculos!
Dessa forma, qualquer travessia de fronteira em nosso mapa nos jogará em uma região pintada com outra cor. Portanto, não haverá regiões adjacentes pintadas com a mesma cor. Se ainda está em dúvida, pode fazer o teste!



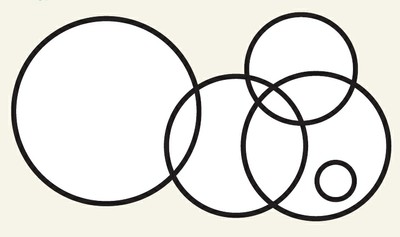

davi
alguem me esplica como colori essa imagem de circulos
Publicado em 23 de fevereiro de 2021
Pedro
Eu também não sei
Publicado em 24 de fevereiro de 2021
Paola🌈
Amei CHC💕eu amo pintar gosto muito de colorir e também gosto de pintar mapas, você pode fazer mais para mim ??? Porque eu amei e também amei o título colorido mapas… tchau CHC👋🏻👋🏻💕🦋
Publicado em 10 de agosto de 2023