
1,2,3… Estes são os números naturais, nesta ordem. Cada um dos naturais tem um único sucessor, obtido quando a ele somamos o 1. Os naturais podem ser pensados como símbolos que representam certas quantidades. Foram e serão sempre necessários para se contar objetos.
Contar um conjunto de objetos é associar a cada um deles um número natural, começando do 1 e indo na seqüência crescente. Isso significa que estamos pondo em cada objeto uma etiqueta identificadora. Ou então podemos pensar que estamos vestindo os objetos com camisetas numeradas, uma para cada objeto diferente. Quando acabamos de fazer isso, ou seja, quando acabamos de contar, o número na camiseta do último objeto é a quantidade de elementos — ou de objetos — do conjunto.
O maior de todos os números, para uma criança, pode ser 100, 1000 ou 10.000.000.000.000. Mas, se nos perguntarmos seriamente sobre o maior número natural, não será difícil perceber que ele não existe. Imaginemos que de fato ele exista e que tenha um nome. Vamos chamá-lo de “longínquo”. Ora, se cada número é sempre seguido por um sucessor, depois do “longínquo” virá “longínquo” + 1, que irá roubar de “longínquo” a qualidade de último e maior de todos os números.
Assim, os números naturais são um exemplo de um conjunto infinito, ou seja, que não tem fim, não acaba nunca. O símbolo do infinito (um “oito deitado”) representa esta idéia de algo a que nunca se chega.
Experimente perguntar a seus amigos o que é infinito e peça exemplos de conjuntos infinitos. Você vai ouvir que são infinitos os grãos de areia na praia, ou o número de gotas no oceano, ou de estrelas no céu. Analisando esses exemplos, podemos entender melhor o que é infinito.
Serão infinitos os grãos de areia da praia de Copacabana? Não sei. Vamos contar. Para isso, temos que ir à praia munidos de uma caixinha de fósforos vazia. Depois, temos que olhar bem a paisagem, calculando aproximadamente as muitas medidas do lugar. O comprimento da orla é de cerca de 5 quilômetros e a extensão da faixa de areia é de mais ou menos 50 metros. Vamos dizer também que a profundidade da camada de areia seja de 100 metros.

Acabado o passeio, voltamos para casa, sem esquecer de encher a caixa de fósforos com areia da praia. Mas faça isso sem apertar os grãos. Limpamos uma mesa bem grande e jogamos sobre ela o conteúdo da caixa de fósforos, espalhando o melhor possível os grãos. A idéia é a de que, sobre a mesa, fique uma camada de areia com uma área calculável e a espessura de apenas um grão.
Depois de estimar a área da camada espalhada, separamos um quadrado de 1 centímetro de lado e contamos, nele, todos os grãos de areia, com a ajuda de uma lupa e um estilete. Isso vai dar um trabalhão, mas depois fica mais fácil. Basta multiplicar a quantidade de areia contada pela área da camada de areia e, depois, pelo volume estimado da praia de Copacabana, mantendo a coerência entre as unidades métricas. Se contarmos 10 milhões de grãos na caixa de fósforos, que deve ter um volume de 10 cm3, obteremos um total de.
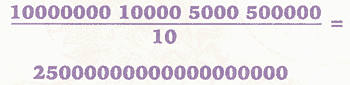
Ou seja, chegamos à ordem de grandeza de 1020 grãos de areia. Pronto. Este é um número finito, que pode até ser escrito num pequeno pedaço de papel.
O artigo acima foi originalmente publicado em
Ciência Hoje na Escola volume 8 – Matemática.
Números naturais e alguns de seus subconjuntos

O conjunto dos números naturais é infinito, como também infinitos são muitos de seus subconjuntos. Basta considerarmos o conjunto que sobra depois de excluirmos o número 1, por exemplo, ou os 10 primeiros números, ou qualquer conjunto finito em que se possa pensar. A surpresa é que o conjunto dos naturais tem subconjuntos infinitos muito diferentes dele mesmo. Observe o quadro abaixo. Cada linha exibe subconjuntos dos naturais, todos eles infinitos.

As duas primeiras linhas mostram o conjunto dos números naturais e o dos pares. Uma contradição aparente logo nos intriga. Se é claro que o tamanho dos naturais (e estamos chamando de tamanho o número total de elementos) é maior que o tamanho dos pares, pela simples razão de que, neste segundo conjunto, faltam todos os números ímpares, também é claro que a cada natural só corresponde um único par, e vice-versa. Basta dividir cada par por 2 para gerar todos os naturais, assim como geramos todos os pares multiplicando os naturais por 2.
Isso quer dizer que cada par pode ser vestido por uma camiseta numerada com um dos números naturais. Mas também cada natural pode ser vestido com uma camiseta de número par. Esses dois conjuntos podem trocar de camisa sem que sobrem camisetas de qualquer um dos dois lados. Assim, não pode haver mais naturais do que pares, e o tamanho dos dois conjuntos tem de ser o mesmo.
Podemos concluir, um pouco surpresos, é claro, que os conjuntos que estão em cada linha do nosso exemplo têm todos o mesmo tamanho, embora retiremos dos naturais, para formar cada um desses conjuntos, um número cada vez maior de elementos. Todos esses conjuntos que podem trocar de camisa com os naturais chamam-se contáveis, ou enumeráveis.
Esse paradoxo sobre os conjuntos infinitos contáveis já preocupava os matemáticos desde os tempos de Galileu, há mais de 300 anos. Mais tarde, ele tornou possível uma definição matemática e definitiva para o infinito.
No final do século passado, Cantor e Dedekind tiraram um proveito dessa aparente contradição própria dos conjuntos infinitos para defini-los. Essa aparente contradição vem do fato de que conjuntos infinitos não respeitam a máxima formulada por Aristóteles, segundo a qual “o todo é sempre maior do que qualquer uma de suas partes”. Como acabamos de ver, o tamanho dos naturais não é maior do que o tamanho dos pares ou de qualquer de seus subconjuntos infinitos, como os ímpares, os múltiplos de 7, as potências de 2 ou de 10.
Um conjunto A é infinito se, e somente se, ele contém outro conjunto, diferente dele mesmo, e os dois podem trocar de camisa.
Essa definição nos diz que, se A é infinito, necessariamente existe B, que é uma parte de A, e que há elementos em A que não estão em B. Mas, apesar disso, a cada ponto de A corresponde um e somente um ponto de B. É estranho, mas essas são coisas do infinito.
Como conseqüência dessa definição, obtemos uma seqüência infinita de infinitos. Pois se A é infinito, então A contém um conjunto infinito, digamos B, e B troca de camisa com A. Então B, por sua vez, também é infinito. Pela mesma definição, B deve conter um outro conjunto, digamos C, que também troca de camisa com B. Por conseguinte, C também será infinito e conterá outro subconjunto infinito, e assim por diante, o que gera uma seqüência infinita de infinitos. Ufa!
Os racionais

Os números racionais (positivos) são o conjunto de todas as frações da forma p/q, em que p e q são dois números naturais quaisquer. Podemos construir os racionais fazendo uma tabela de dupla entrada, na qual as colunas representariam os numeradores, e as linhas, os denominadores. Observe que há números repetidos, infinitas vezes, nessa tabela.

Primeiro, podemos notar que aparentemente há muito mais racionais do que naturais, já que, entre quaisquer dois naturais consecutivos, encontramos uma infinidade de racionais. Por exemplo, entre 5 e 6, temos todos os números da forma 5 + i/n, para qualquer natural i < n. Se n = 10, temos:Primeiro, podemos notar que aparentemente há muito mais racionais do que naturais, já que, entre quaisquer dois naturais consecutivos, encontramos uma infinidade de racionais. Por exemplo, entre 5 e 6, temos todos os números da forma 5 + i/n, para qualquer natural i < n. Se n = 10, temos:
![]()
Observando a tabela dos racionais acima, pode-se esperar que o tamanho dos racionais seja igual ao quadrado do tamanho dos naturais, já que o número de elementos numa tabela de dupla entrada (finita) é calculado multiplicando-se o número de elementos das linhas pelo das colunas. Esperamos, portanto, que o tamanho dos racionais seja maior que o dos naturais.
Mas uma outra surpresa do infinito nos aguarda. Seguindo as setas desenhadas na tabela dos racionais, podemos contar todos os racionais, sem perder nenhum. Isso é um espanto!
Assim, estabelecemos uma correspondência entre os racionais e os naturais e podemos garantir que eles também trocam de camisa entre si. Parece que os infinitos todos trocam de camisa. Mesmo com a potenciação, os infinitos permanecem invariantes, contáveis. E temos uma álgebra estranha:
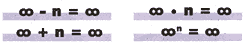
Será, então, que todos os infinitos têm o mesmo tamanho? Afinal, são todos o mesmo infinito? Ou não? A resposta a essas perguntas foi dada há mais de 100 anos por George Cantor, que demonstrou que nem todo infinito tem o mesmo tamanho. Mas essa é uma outra história.




Anna Elise
Achei legal e ao mesmo confuso!
Publicado em 26 de janeiro de 2019
Fernando Netto
Interessante e aterrorizante, risos.
Publicado em 31 de agosto de 2020
Marcelo Gliosci Teixeira
Cantor mostrou, usando a Diagonal de Cantor, que os números Reais formam um infinito maior que o dos Naturais e Racionais.
Publicado em 24 de março de 2021
Mariana?
Muito legal não sabia disso 🙂
Publicado em 10 de maio de 2022